こんにちは、エンジニアのオオバです。
この記事ではUnityを使って球メッシュをプログラミングで作ってみます。

↑上のような球です。一見ハードルが高く感じるかもしれません。もちろん三角形よりは難しいですが、地道に1つずつ頂点の配置と順序を考えていけば理解できます。
注意点ですが、今回紹介する球の作り方は「完全に我流」です。もっとシンプルな実装があるかもしれません。

本記事では説明しやすいように、分割数を少なくしています。横分割6、縦分割4です。
(上から見たら正六角形、横から見たら4つの面が縦に並んでいる状態です)

上の図のとおり「天面」「側面」「底面」の3つに分けて「頂点座標配列」と「インデックス配列」を作ります。
少しおさらいすると、Unityプログラミングでメッシュを作るためには 「Vector3型の頂点座標配列」 と 「インデックス配列」 が必要です。この辺りを復習してから臨みたい方は、こちらの記事がおすすめです。かなり丁寧に 3Dプログラミングの基礎 を解説しています。
👉DOTweenの教科書を読んでUnityアニメーションをプログラミングしてみよう!
球の作成手順
球を作る手順は以下です。
1.「天面」の「頂点座標配列」
2.「側面」の「頂点座標配列」
3.「底面」の「頂点座標配列」
4.「天面」の「インデックス配列」
5.「側面」の「インデックス配列」
6.「底面」の「インデックス配列」
球の頂点座標配列の作成
球の頂点座標配列を作っていきます。その前に、今回実装する球には以下のパラメーターを変更できるようにしました。
| 変数名 | 内容 |
|---|---|
| r | 球の半径 |
| divideX | 球の横の分割数 |
| divideY | 球の縦の分割数 |
分割数値を上げれば、、それだけなめらかな球が出来上がります。
球の各頂点座標の算出方法
球の各頂点座標の算出方法を解説します。まずは簡単な上下の頂点から。変数は「r」は半径です。上頂点の座標は (0, r, 0) 、 下頂点の座標は (0, -r, 0) です。
問題は側面の頂点です。分かりやすく図解して解説します。まずは球を「側面」から見てみましょう。
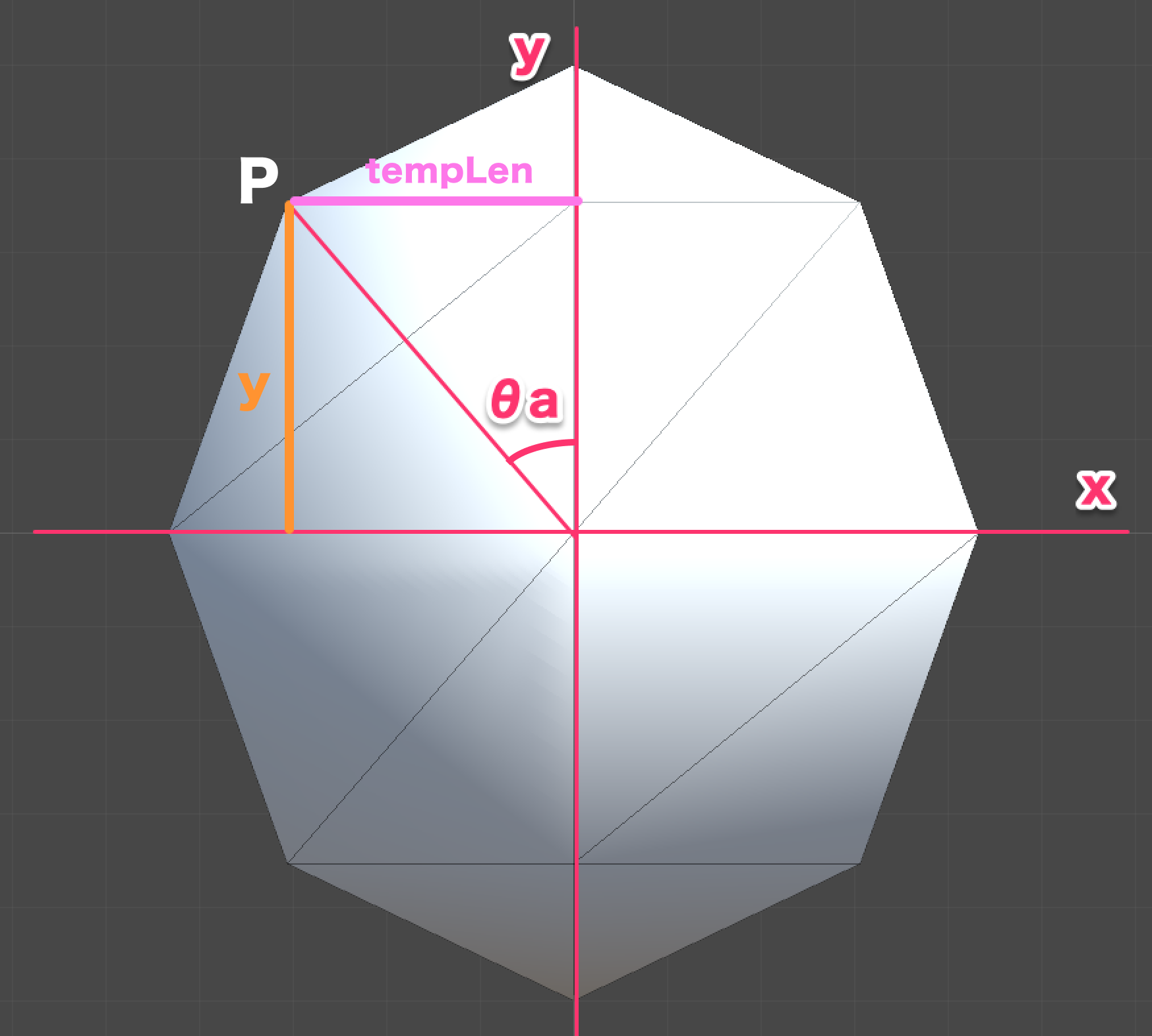
側面頂点Pの座標を算出してみます。「θa」は180度 / 縦分割数(ここでは4)で算出した角度(この場合45度)です。オレンジのラインが頂点Pのy座標になります。計算式は y = r * consθa です。
薄いピンクは頂点Pの高さにおける円の半径になります。この値を使い、x座標、z座標を割り出し際に使用します。ここでは「tempLen」としておきます。 tempLen = r * sinθa です。
次に球を上から見てみます。

「θb」は 360度 / 横分割数 で算出した中心角です。緑ラインがx座標、青ラインがz座標ということになります。側面から見たときに算出した「tempLen」を使って頂点PのX、Z座標を計算します。
x = tempLen * sinθb 、z = tempLen * cosθb となります。
この処理を分割数の回数for文で実行するのです。縦の分割数に関しては、天面、底面は別の処理なので、その分for文の回数を減らす必要があります。
| 座標 | 計算式 |
|---|---|
| x | tempLen * sinθb |
| y | r * consθa |
| z | tempLen * cosθb |
※rは半径、tempLen = tempLen = r * sinθaです。
頂点座標配列を算出するコードはこちらです。
// 半径(ここでは仮に1メートル)
float r = 1f;
int cnt = 0;
int vertCount = divideX * (divideY - 1) + 2;
var vertices = new Vector3[vertCount];
// 中心角
float centerRadianX = 2f * Mathf.PI / (float) divideX;
float centerRadianY = 2f * Mathf.PI / (float) divideY;
// 天面頂点座標を追加
vertices[cnt++] = new Vector3(0, r, 0);
for (int vy = 0; vy < divideY - 1; vy++)
{
var yRadian = (float) (vy + 1) * centerRadianY / 2f;
// 1辺の長さ
var tempLen = Mathf.Abs(Mathf.Sin(yRadian));
var y = Mathf.Cos(yRadian);
for (int vx = 0; vx < divideX; vx++)
{
var pos = new Vector3(
tempLen * Mathf.Sin((float) vx * centerRadianX),
y,
tempLen * Mathf.Cos((float) vx * centerRadianX)
);
// サイズ反映
vertices[cnt++] = pos * r;
}
}
// 底面頂点座標を追加
vertices[cnt] = new Vector3(0, -r, 0);
これで頂点座標配列は作成完了しました。次にインデックス配列の作成入ります。
球のインデックス配列の作成
頂点座標配列より、インデックス配列の方が複雑です。重要なのは頂点のインデックス番号を頭の中で把握しておくこと。

再び球を上から見て見ましょう。イメージしやすいように頂点番号を割り振ってみました。
球の天面のインデックス配列の作成

緑の部分の天面の頂点インデックス配列を作っていきます。
天面は全て三角形なので想像しやすく、以下のような配列になるようにします。
0, 1, 2,
0, 2, 3,
0, 3, 4,
~~~略~~~
0, 6, 1
必ず0始まりのインデックス配列になります。コードはこんな感じです。
// indicesはインデックス配列
// divideX*3・・・分割数分の三角形を作成するために、三角形に必要な頂点数3を乗算する
for (int i = 0; i < divideX * 3; i++)
{
if (i % 3 == 0)
{
// 天面の出っ張り
indices[cnt++] = 0;
}
else if (i % 3 == 1)
{
indices[cnt++] = 1 + offsetIndex;
}
else if (i % 3 == 2)
{
var index = 2 + offsetIndex++;
// ループさせるためにindices[1]を使う
index = index > divideX ? indices[1] : index;
indices[cnt++] = index;
}
}
このように「0」始まりで三角形を作っていきます。注意点は1つだけ。最後の三角形 「0, 6, 1」 の部分の最後のインデックスは 1 を使っているところです。
球の側面のインデックス配列の作成
次に緑部分の側面のインデックス配列の作り方に入ります。

上の画像は側面の一部ですが、他側面も実装する内容は同じです。

①〜⑥の順にインデックス配列を作っていきます。

①から見ていきます。
1, 7, 8,
1, 8, 2
上の順に頂点を結んで、三角形を2つ作ります。四角形を一つ作り終えたら、開始のインデックス値を「1」加算して同じ処理を走らせます。
この部分のコードはこんな感じになります。
// 開始Index
startIndex = indices[1];
for (int i = 0; i < sideIndexLen; i++)
{
if (i % 6 == 0 || i % 6 == 3)
{
indices[cnt++] = startIndex;
}
else if (i % 6 == 1)
{
indices[cnt++] = startIndex + divideX;
}
else if (i % 6 == 2 || i % 6 == 4)
{
indices[cnt++] = startIndex + divideX + 1;
}
else if (i % 6 == 5)
{
indices[cnt++] = startIndex + 1;
// 四角形を作り終えたら開始インデックス値を1加算
startIndex++;
}
}
ただ、上記のコードでは、次の⑥の四角形のインデックスを取得できません。

- 1周した時(⑥のIndex)、ループさせるために1, 7を取得する
- 1周した後、次の側面のIndexを取得する
それらを諸々考慮したコードは次になります。
// 開始Index番号
int startIndex = indices[1];
// 天面、底面を除いたIndex要素数
int sideIndexLen = divideX * (divideY - 2) * 2 * 3;
// 1最後の四角形を作るときに必要な最後のIndex
int lap1stIndex = 0;
// 1最後の四角形を作るときに必要な最後から2番目のIndex
int lap2ndIndex = 0;
// 一周したときのindex数
int lapDiv = divideX * 2 * 3;
int createSquareFaceCount = 0;
for (int i = 0; i < sideIndexLen; i++)
{
// 一周の頂点数を超えたら更新(初回も含む)
if (i % lapDiv == 0)
{
lap1stIndex = startIndex;
lap2ndIndex = startIndex + divideX;
createSquareFaceCount++;
}
if (i % 6 == 0 || i % 6 == 3)
{
indices[cnt++] = startIndex;
}
else if (i % 6 == 1)
{
indices[cnt++] = startIndex + divideX;
}
else if (i % 6 == 2 || i % 6 == 4)
{
if (i > 0 &&
(i % (lapDiv * createSquareFaceCount - 2) == 0 ||
i % (lapDiv * createSquareFaceCount - 4) == 0)
)
{
// 1周したときのループ処理
// 最後から2番目のIndex
indices[cnt++] = lap2ndIndex;
}
else
{
indices[cnt++] = startIndex + divideX + 1;
}
}
else if (i % 6 == 5)
{
if (i > 0 && i % (lapDiv * createSquareFaceCount - 1) == 0)
{
// 1周したときのループ処理
// 最後のIndex
indices[cnt++] = lap1stIndex;
}
else
{
indices[cnt++] = startIndex + 1;
}
// 開始Indexの更新
startIndex++;
}
else
{
Debug.LogError("Invalid : " + i);
}
}
底面の頂点インデックス配列の作成
最後に底面のインデックス配列を作ります。

以下のような配列になります。
13, 14, 19,
14, 15, 19,
15, 16, 19,
~~~~略~~~~~
17, 18, 19
天面とほぼ同じなので、説明は割愛しますが、コードは以下のようになります。
// 底面Index
offsetIndex = vertices.Length - 1 - divideX;
// 1周したときのループIndex
var loopIndex = offsetIndex;
for (int i = divideX * 3 - 1; i >= 0; i--)
{
if (i % 3 == 0)
{
// 底面の先頂点
indices[cnt++] = vertices.Length - 1;
offsetIndex++;
}
else if (i % 3 == 1)
{
indices[cnt++] = offsetIndex;
}
else if (i % 3 == 2)
{
var value = 1 + offsetIndex;
if (value >= vertices.Length - 1)
{
value = loopIndex;
}
indices[cnt++] = value;
}
}
最後にこれらの配列をMeshインスタンスにセットして描画します。この辺りは以前の記事を参考にしてください。
ソースコード全文は記事後半の「→ ソースコード全文」で公開していますので、ぜひそちらをどうぞ。

このようにメッシュの分割数も変更することもできます。
まとめ
今回は球のメッシュを動的に描画してみました。天面、側面、底面の順に「頂点座標配列」と「インデックス配列」を作ります。少し難しかったかもしれません。やはり、球の分割数を減らして考えると理解しやすいのでおすすめです。
ところで、今回作成した球には「UV座標」を書き込んでいません。つまり、この球にテクスチャは貼れないということです。
メッシュをプログラミングで作る、3Dプログラミングをやってみたい方はぜひ、挑戦してみてください。自分で考えて見ることはとても効率の良い学習です。
次はぜひ「カプセルメッシュ」に挑戦してみてください。カプセルは球の応用で理解しやすいです。次の記事をあわせて読むことで効率よく3Dプログラミングを学べます。
今回の記事がまだ良くわからなかった方は、こちらの記事を参考に復習してみてください。最初は三角形を完璧に理解することが大事ですね。
ソースコード全文
今回作成したソースコードはC#ファイル1つだけです。少し長めのコードですが、ほとんどは球のインデックス配列を作成処理です。
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class Sphere : MonoBehaviour
{
private MeshRenderer _renderer;
private MeshRenderer Renderer => _renderer != null ? _renderer : (_renderer = GetComponent<MeshRenderer>());
private MeshFilter _filter;
private MeshFilter Filter => _filter != null ? _filter : (_filter = GetComponent<MeshFilter>());
private Mesh _mesh;
void Start()
{
Create();
}
public Vector2Int divide;
void Create()
{
int divideX = divide.x;
int divideY = divide.y;
var data = CreateSphere(divideX, divideY);
if (_mesh == null)
_mesh = new Mesh();
_mesh.SetVertices(data.vertices);
_mesh.SetIndices(data.indices, MeshTopology.Triangles, 0);
Filter.mesh = _mesh;
_mesh.RecalculateNormals();
}
struct MeshData
{
public Vector3[] vertices;
public int[] indices;
}
MeshData CreateSphere(int divideX, int divideY, float size = 1f)
{
divideX = divideX < 4 ? 4 : divideX;
divideY = divideY < 4 ? 4 : divideY;
// =============================
// 頂点座標作成
// =============================
// 半径
float r = size * 0.5f;
int cnt = 0;
int vertCount = divideX * (divideY - 1) + 2;
var vertices = new Vector3[vertCount];
// 中心角
float centerRadianX = 2f * Mathf.PI / (float) divideX;
float centerRadianY = 2f * Mathf.PI / (float) divideY;
// 天面
vertices[cnt++] = new Vector3(0, r, 0);
for (int vy = 0; vy < divideY - 1; vy++)
{
var yRadian = (float) (vy + 1) * centerRadianY / 2f;
// 1辺の長さ
var tmpLen = Mathf.Abs(Mathf.Sin(yRadian));
var y = Mathf.Cos(yRadian);
for (int vx = 0; vx < divideX; vx++)
{
var pos = new Vector3(
tmpLen * Mathf.Sin((float) vx * centerRadianX),
y,
tmpLen * Mathf.Cos((float) vx * centerRadianX)
);
// サイズ反映
vertices[cnt++] = pos * r;
}
}
// 底面
vertices[cnt] = new Vector3(0, -r, 0);
// =============================
// 頂点インデックス作成
// =============================
int topAndBottomTriCount = divideX * 2;
// 側面三角形の数
int aspectTriCount = divideX * (divideY - 2) * 2;
int[] indices = new int[(topAndBottomTriCount + aspectTriCount) * 3];
//天面
int offsetIndex = 0;
cnt = 0;
for (int i = 0; i < divideX * 3; i++)
{
if (i % 3 == 0)
{
indices[cnt++] = 0;
}
else if (i % 3 == 1)
{
indices[cnt++] = 1 + offsetIndex;
}
else if (i % 3 == 2)
{
var index = 2 + offsetIndex++;
// 蓋をする
index = index > divideX ? indices[1] : index;
indices[cnt++] = index;
}
}
// 側面Index
/* 頂点を繋ぐイメージ
* 1 - 2
* | |
* 0 - 3
*
* 0, 1, 2
* 0, 2, 3
*
* 注意 : 1周した時にループするのを忘れないように。
*/
// 開始Index番号
int startIndex = indices[1];
// 天面、底面を除いたIndex要素数
int sideIndexLen = divideX * (divideY - 2) * 2 * 3;
// ループ時に使用するIndex
int loop1stIndex = 0;
int loop2ndIndex = 0;
// 一周したときのindex数
int lapDiv = divideX * 2 * 3;
int createSquareFaceCount = 0;
for (int i = 0; i < sideIndexLen; i++)
{
// 一周の頂点数を超えたら更新(初回も含む)
if (i % lapDiv == 0)
{
loop1stIndex = startIndex;
loop2ndIndex = startIndex + divideX;
createSquareFaceCount++;
}
if (i % 6 == 0 || i % 6 == 3)
{
indices[cnt++] = startIndex;
}
else if (i % 6 == 1)
{
indices[cnt++] = startIndex + divideX;
}
else if (i % 6 == 2 || i % 6 == 4)
{
if (i > 0 &&
(i % (lapDiv * createSquareFaceCount - 2) == 0 ||
i % (lapDiv * createSquareFaceCount - 4) == 0)
)
{
// 1周したときのループ処理
// 周回ポリゴンの最後から2番目のIndex
indices[cnt++] = loop2ndIndex;
}
else
{
indices[cnt++] = startIndex + divideX + 1;
}
}
else if (i % 6 == 5)
{
if (i > 0 && i % (lapDiv * createSquareFaceCount - 1) == 0)
{
// 1周したときのループ処理
// 周回ポリゴンの最後のIndex
indices[cnt++] = loop1stIndex;
}
else
{
indices[cnt++] = startIndex + 1;
}
// 開始Indexの更新
startIndex++;
}
else
{
Debug.LogError("Invalid : " + i);
}
}
// 底面Index
offsetIndex = vertices.Length - 1 - divideX;
var loopIndex = offsetIndex;
for (int i = divideX * 3 - 1; i >= 0; i--)
{
if (i % 3 == 0)
{
// 底面の先頂点
indices[cnt++] = vertices.Length - 1;
offsetIndex++;
}
else if (i % 3 == 1)
{
indices[cnt++] = offsetIndex;
}
else if (i % 3 == 2)
{
var value = 1 + offsetIndex;
if (value >= vertices.Length - 1)
{
value = loopIndex;
}
indices[cnt++] = value;
}
}
return new MeshData()
{
indices = indices,
vertices = vertices
};
}
}
この記事は以上です。球は少し難しかったかもしれませんが、理解できると自分で好きなメッシュを作れるようになります。少しずつで良いので勉強してみてください。

筆者のXをフォローしよう
Unityオブジェクトの描画順の制御って難しいですよね。
この度、Unityの描画順を体系的に学べる「Unity描画順の教科書」を執筆しました。
Unityの描画順を基礎から学びたい方はぜひ確認してみてください!
→ Unity描画順の教科書
最後まで読んでいただきありがとうございました!
すばらしい3Dプログラミングライフをお過ごしください。
- Unity2021.3.0f1













